Local Features

transformation을 해도 invariant한 feature들을 찾는다
geometric invariance는 translation, rotation, scale
photometric invariance는 brightness, exposure 등이 있다
이미지에서 이러한 feature를 transform, shear 등으로 매칭해본다
photometric은 빛에 의해서 달라지므로 global한 정도로는 어렵다
★ Advantages of local features
Locality(지역성) : 특징이 지역적으로 차폐와 혼잡에 강하다
Distinctiveness(독특성) : 큰 데이터베이스의 객체들을 구별할 수 있다
Quantity(수량) : 단일 이미지에서 수백 개 또는 수천 개의 특징을 추출할 수 있다
Efficiency(효율성) : 실시간 성능을 달성할 수 있다
Generality(일반성) : 다양한 상황에서 다양한 유형의 특징을 활용할 수 있다
Primitive Features: Edges and Corners
What causes an edge?
Depth discontinuity(깊이 불연속성) : 물체간 depth가 달라지는 경우
Surface orientation discontinuity(표면 방향 불연속성) : 표면의 방향이 수직하게 달라지는 경우
Reflectance discontinuity(반사율 불연속성) : 표면 재질이 달라지는 경우
Illumination discontinuity(조명 불연속성) : 그림자 등
Detecting edges
edge : intensity가 급격하게 변하는 것
intensity의 급격한 변화를 찾기 위해서 gradient operator를 사용한다
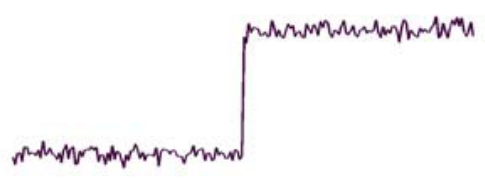

noise가 있으면 모든 부분에서 미분값이 높아지기 때문에 gradient하기 전에 smoothing을 한다
1차 derivative(미분)에서는 최대값이 edge이다
2차 미분에서는 0을 지나는 부분이 edge이다
각각은 filter를 만드는 과정에서 결합법칙을 사용한다
Convolution
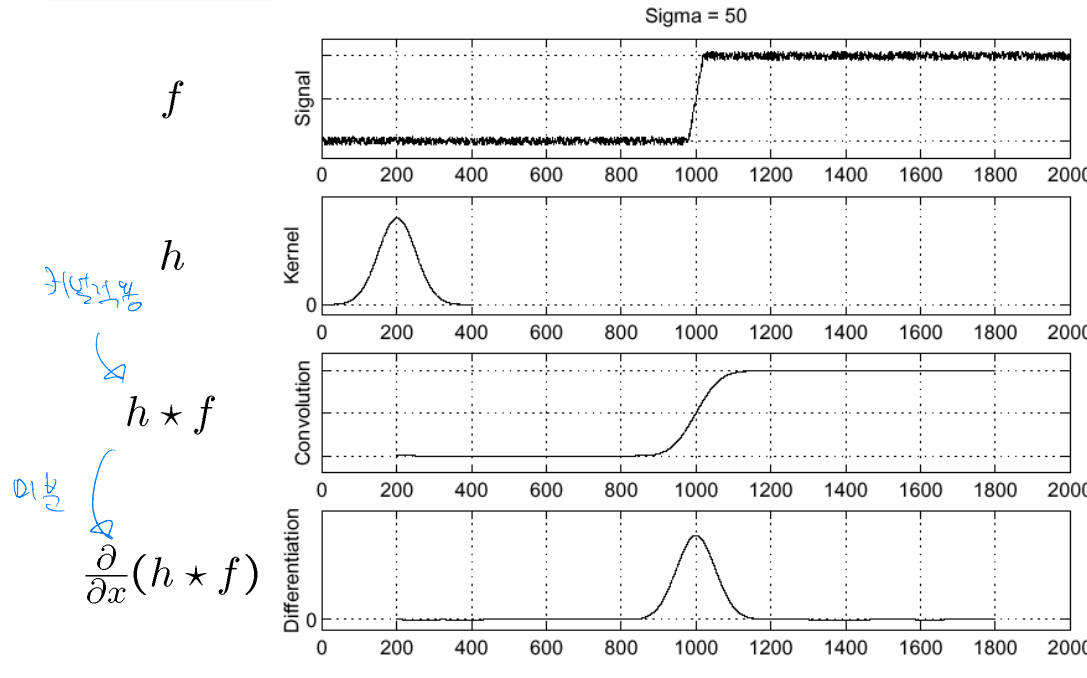
gaussian kernel을 이용해서 convolution을 한 후 미분한다
DoG(Derivation of Gaussian)
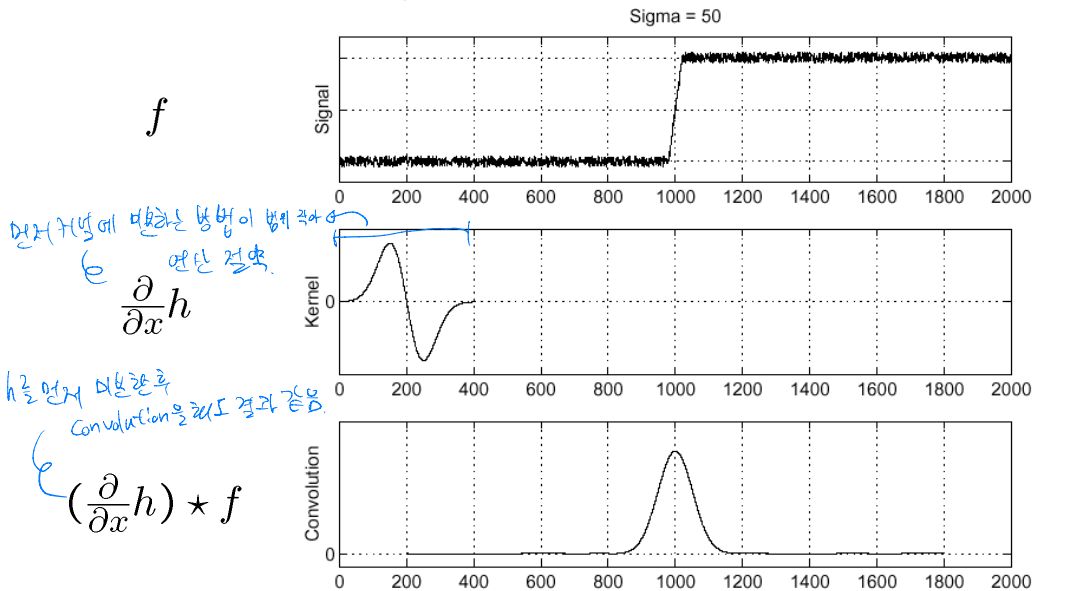
일반적인 convolution과 달리 먼저 gaussian kernel을 미분하는 방법이다
kernel을 먼저 미분하면 미분 연산을 하는 범위가 줄어든다
결합법칙이 성립하므로 kernel을 먼저 미분하고 convolution을 하여도 결과는 같다
LoG(Laplacian of Gaussian)

gaussian을 2차 미분한 LoG를 kernel로 사용한다
0이 되는 점을 찾으면 edge이고, 이산적인 경우 0이 안나오면 곱이 음수인 zero crossing을 찾는다
Gradient
\(I(X,Y)\)를 digital image라고 한다
\(I_X(X,Y), I_Y(X,Y) \) 각 x,y 방향에 대한 편미분을 한다
이를 각각 \(I_X,I_Y\)라고 한다
vector [\(I_X,I_Y\)] 가 gradient로 변화량을 의미한다
gradient를 magnitude하여 구한 scalar \(\sqrt{I_X^2+I_Y^2}\) 가 변화량의 크기이다
edge normal \(arctan(\frac{I_Y,I_X})\) 를 구하여 edge의 방향을 구한다
Canny Edge Detection
step
1. DoG(Derivative of Gaussian)을 적용한다
2. Non-maximum suppresion
- multi-pixel 너비의 ridges을 single pixel width로 줄인다

3. linking and thresholding
- low, high edge 강도에 대한 threshold 설정
- 높은 threshold를 초과하는 edge에 연결된 모든 낮은 threshold 이상의 edge를 accept한다
★ Finding Corners
edge detector는 corner에서 성능이 안좋다
corner를 알아내는 것은 매칭에 반복적으로 사용되는 점을 찾기에 필요하다
idea
corner에서는 gradient가 명확하지 않다
corner 주변 영역에서는 gradient가 두 개 이상의 서로 다른 값을 가진다
Harris corner detector

feature의 고유성을 나타내는 local을 측정한다
corner에서는 윈도우를 이동할 때 어느 방향으로 이동해도 큰 변화가 생긴다


움직임을 shift [u,v]라고 하고 이미지 area [x,y]에서 이루어진다
edge의 방향과 u,v의 방향이 다르면 차이가 크다
주어진 영역 [x,y]에서 [u,v] 이동할 때 intensity의 변화

intensity I에 대한 테일러 급수는 2차 이상은 날린다
차수가 높으면 fine한 detail을 다룰 수 있지만,
shift [u,v]가 작으면 1차 근사로 충분하기 때문이다
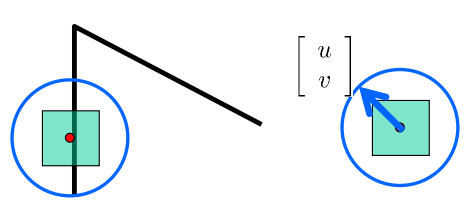
녹색 창의 중심을 파란 원 위의 어느 곳이든 이동 가능하다

이미지 intensity의 변화량 E에 대해서
가장 큰 E값과 작은 E값은 행렬 H의 eigenvector를 찾으면 알 수 있다
Eigenvector
$$Ax = \lambda x$$
행렬 A 곱했을 때 원래 vector와 차이가 나는 것이 오직 곱한 scalar \(\lambda\)만큼인 0이 아닌 vector
방향을 바뀌지 않는 벡터를 찾으면 eigenvector이다

A 행렬을 곱하면 red vector는 바뀌고 blue vector는 그대로이다
blue vector가 eigenvector이고 eigenvalue는 1이다
harris corner detector에서 eigenvector를 구하는 람다를 비교하면 edge인지 corner인지 알 수 있다
람다가 둘 다 작으면 flat
한 쪽이 크면 edge
둘 다 크면 corner이다
Advanced Features: SIFT
Invariance
두 이미지 \(I_1, I_2\)가 있다
\(I_2\)는 \(I_1\)이 transform된 것이다
transform에 관계없이 동일한 특징을 invariance라고 하는데
translation, 2D rotation, scale의 feature들은 invariant하게 설계 되어있다
제한된 3D rotation (SIFT는 60도까지)
제한된 affine transformation
제한된 illumination / contrast 변화
등이 invariance한 feature들이다
How to achieve invariance
1. detector가 invariant하도록 한다
harris corner detector는 translation과 rotation에서 invariant하다
scale은 까다로운데,
일반적으로는 gaussian pyramid를 사용해서 여러 scale에서의 feature를 detect한다 (MOPS: Multi-Scale Oriented Patches)
더 정교한 방법으로 각 feature를 나타내는 best scale을 찾는다 (SIFT: Scale Invariant Feature Fransform)
2. invariant feature descriptor를 설계한다
descriptor는 detect된 feature point 주변 영역의 정보를 포착한다
가장 간단한 descriptor는 pixel의 정사각형 window이다
Types of invariance
- Illumination
- Scale
- Rotation
- Affine
- Full Perspective 카메라 방향
★ How to achieve scale invariance

Pyramids
width와 height를 2로 나눈다
각 픽셀에 대해서 4개의 픽셀 평균을 취한다 (혹은 gaussian blur를 사용한다)
이미지가 매우 작아질 때까지 반복한다
각 크기의 이미지에 필터를 적용한다
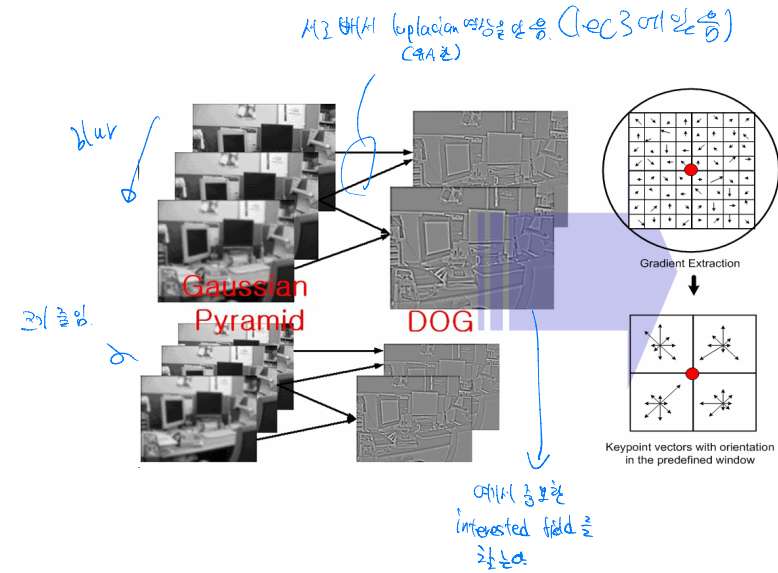
Scale Space (DOG method)
pyramid와 유사하지만 blur 처리된 이미지로 간격을 채운다
비용을 들이지 않고도 linear scaling을 하는 것과 같다
이러한 이미지들의 difference에서 feature를 추출한다
Difference of Gaussians 사이에 feature가 반복적으로 존재하면,
scale invariant한 것이므로 유지해서 표현한다
scale invariance 순서
Gassian Pyramid → DOG(Difference Of Gaussian) → Gradient Extraction → vector orientation
Rotation Invariance
모든 feature를 동일한 방식으로 rotation해서 일정하게 정렬한다
gradient 방향의 histogram을 만든다
가장 주요한 방향으로 회전시킨다
Multiscale Oriented PatcheS descriptor (MOPS)

detected feature 주변 정사각형 40x40 window를 잡는다
scale을 1/5로 줄인다
수평으로 회전시킨다
feature를 중심으로 8x8 정사각형 window를 샘플링한다
window 내에서 평균을 빼고 표준 편차로 나누어거 intensity를 normalize한다
window의 gradient를 구한 후 weighted histogram으로 표현한다
Scale Invariant Feature Transform (SIFT) Step
- Scale-space Pyramid Extrema Detection
- Keypoint Localization
- Orientation Assignment
- SIFT Descriptor Generation
Build Scale-Space Pyramid
DOG(Difference of Gaussian)을 계산하여 Gaussian 피라미드를 생성한다
Key Point Localization
scale 공간에서 DOG를 통해 key point 후보가 되는 극대 극소 값을 찾는다
찾은 후보 중 scale 샘플링을 하여 key point 위치를 조정한다
Orientation Assignment
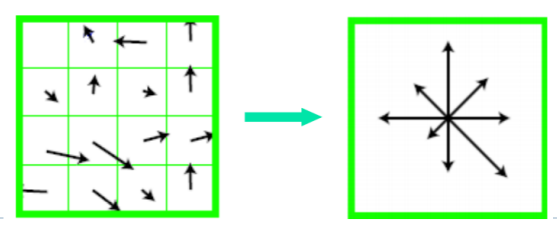
key point 주변의 gradient를 계싼하여 크기와 방향을 구하고
화살표가 중심으로부터 시작하는 histogram을 만든다
Scale Invariant Feature Transform (SIFT)
key point에서 16x16 이웃 내의 상대적인 방향과 크기를 계산한다
4x4 영역에 대해서 weighted histogram을 형성한다
magnitude 및 spatial gaussian으로 weight를 부여한다
16개의 histogram을 하나의 긴 128차원 vector로 연결한다

8x8에서 2x2 descriptor의 경우 위와 같이 바뀐다
SIFT descriptor
full version
16x16 윈도우를 4x4 grid cell로 나눈다
각 cell에 대해서 orientation histogram을 계산한다
16개의 cell * 8개의 orientation = 128개의 descriptor
Feature Matching
후보 점들끼리 비교하여 distance가 최소화되는 점이 matching point이다
True/false positives
distance threshold가 영향을 미친다
true positives는 올바르게 검출된 match 수
false positives는 잘못 검출된 match 수
Evaluating the results
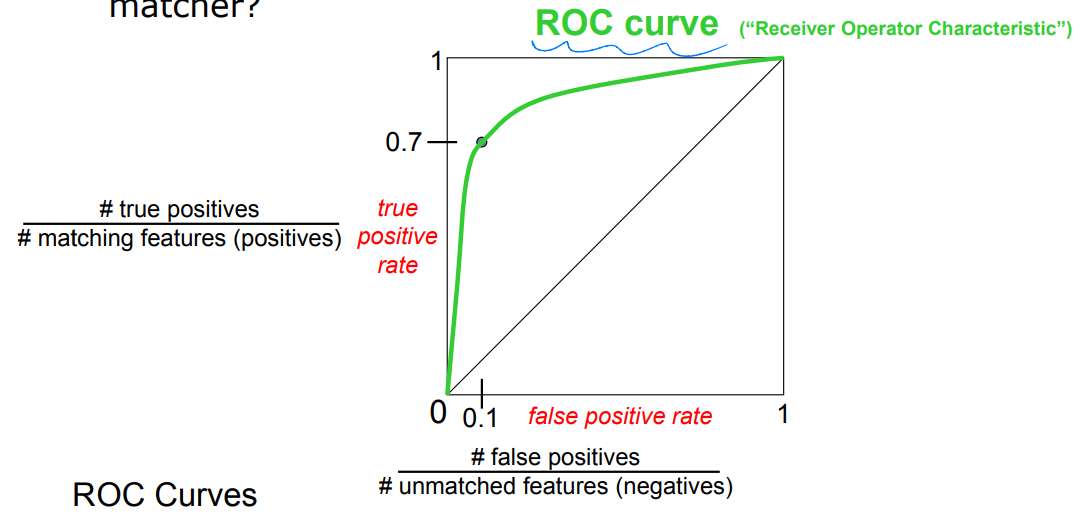
각 threshold에 대해서 true positive rate(TPR), false positive rate(FPR)를 계산해서 ROC curve를 구해서 성능을 평가한다
ROC curve
다양한 threshold에 대해서 올바른 match와 잘못된 match를 계산해서 생성된다
곡선 아래 면적을 AUC라고 하는데 이를 최대화하는 것이 목표
AUC는 feature matching 방법들을 비교하는 지표




