1.2 표기법와 정의
먼저 이 책에서 사용하는 수학적 표기법을 설명할 것이다. 이 section에서 설명하는 많은 단어를 비롯하여, 이 책에서 계속해서, realtimerendering.com에서의 선형대수 부록을 참고하라.
1.2.1 수학적 표기법
Table 1.1은 여기서 사용할 대부분의 수학적 표기에 대한 요약이다. 그 중 몇 개의 개념은 여기서 길게 설명한다.
예외적으로 어떤 규칙들은 표에 나오지 않는데, 방사 휘도 L이나 방사 위도 E, 그리고 산란 계수 σ_s 등 문헌에 극도로 자주 나오는 개념인 primarily shading equations가 그렇다.
각도와 스칼라는 실수계 R에서 다뤄진다. Vectors와 points는 볼드체로 표현된다. 그 요소들에 대한 접근은
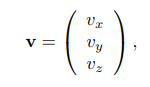
위와 같은 column vector 형태로 표현한다. column vector는 컴퓨터 그래픽스계에서 흔히 쓰인다. 가끔 (v_x, v_y, v_z)와 같은 형태로 사용될 텐데, 이는 단지 읽기 쉬워서이다. (형식적으로는 (v_x, v_y, v_z)^T가 맞는 표현이다)
[※ 작성의 편의를 위하여 아래첨자는 '_', 위첨자는 '^'로 표현]

homogeneous 개념을 사용하면, 좌표는 4개의 값으로 다음과 같이 표현된다.


vector는 위와 같이
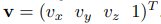
point는 위와 같이 표현한다.
가끔 벡터나 점에 요소를 세 개만 사용할 때도 있으나, 애매한 일이 없도록 이와같이 표현한다.
예를들어 행렬을 다룰 때, 벡터나 점에 대한 표기법이 같으면 굉장히 유리하다. Chap 4의 transforms에서도 그렇다. 어떤 알고리즘에서는

x, y, z를 사용하는 것보다 위 식처럼 numeric indices를 사용하는 것이 편리할 것이다.
이러한 벡터와 점에 대한 규칙들은 two-element vectors에 대해서도 그렇다. 이 경우엔, three-element vector의 마지막 요소를 생략한다.
행렬은 더 설명이 필요하다. 가장 흔히 쓰이는 것은 2 × 2, 3 × 3, 4 × 4의 형태이다.
3 × 3 행렬 M의 접근 방식을 보자. 이 방법으로 간단히 다른 크기로 확장할 수 있다. M의 스칼라값은 m_ij로 표현되고, i와 j는 0 ≤ (i,j) ≤ 2 이다. i는 row, j는 column을 의미한다.
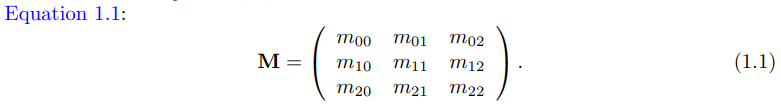
밑의 표기법에서는 3 × 3 행렬인 M을 분리하고, m_,j는 j번째 column vector를, m_i,는 i번째 row vector를 나타낸다. 벡터와 점에 따라 column vector에 순서를 매기는 것이 x, y, z, w로 표현될 수도 있다.

plane

plane은 위와 같이 표현되고, 수학적인 형태를 가지고 있다. plane normal n 과 scalar d가 그렇다. normal은 vector가 묘사하는 plane이 보는 방향이다. 곡면처럼 일반적인 경우에 normal은 이 방향을 바라보는 표면의 특정 point를 의미한다. plane에서 같은 normal은 모두 이 point를 사용한다. π 는 흔히 plane의 수학적 표기법으로 쓰인다. plane π는 n * x + d > 0인 positive half-space와 n * x + d < 0인 negative half-space로 구분된다. 나머지 모든 points는 plane 안에 있는 점들이다.
triangle은 세 개의 점인 v_0, v_1, v_2로 정의되고,
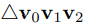
위와 같이 표현한다.
아래의 표는 추가적인 수학적인 연산나와 그 표기법이 나와있다. dot, cross, determinant(행렬식), length 연산자들은 realtimerendering.com 의 선형대수 부록에서 볼 수 있다. transpose operator는 column vector를 row vector and vice versa(row vector로 바꾸고 element 순서를 거꾸로 하는 것. T를 이용한 전치행렬인듯)로 바꿔준다.

그래서 column vector는 위 그림과 같은 형태로 바꿀 수 있다. 표에서의 Operator 4, (introduced in Graphics Gems IV)는 two-dimensional vector의 unary operator(단항 연산자)이다.


위 벡터 v에 Operator 4를 취하면

위와 같은 v의 perpendicular(수직) vector를 얻을 수 있다.
scalar a의 절댓값을 |a|로 정의하고, 행렬 A의 determinant(행렬식)을 구하기 위해 |A|를 사용한다. 때로는 |A| = (a b c) = det(a,b,c)로 a,b,c가 각각 행렬 A의 벡터일 때 사용하기도 한다.
Operator 8,9 는 shading calculations(광연산)을 할 때 사용하는 clamping operator이다.

Operator 8을 통해 음의 값을 0으로 clamp 연산하면 위와 같다.
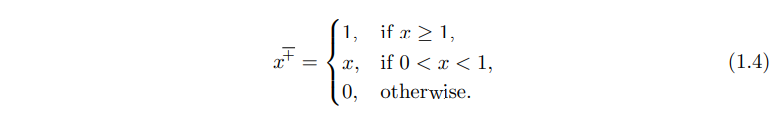
Operator 9을 통해 0~1 사이의 값을 clamp 연산하면 위와 같다.
Operator 10은 팩토리얼이다.

Operator 11은 binomial factor(이항 계수)이다.

x = 0, y = 0, z = 0인 평면을 coordinate planes(좌표평면)이나 axis-aligned planes(축이 포함된 평면)이라고 한다.

위 세 축은 main axes, main directions 라고 불리며, 각각 x-axis, y-axis, z-axis라고 부른다. 이 축들은 standard basis라고 부르기도 한다. 다른 서적과는 다르게 여기서는 orthonormal bases(벡터의 수직 요소로 구성)라고 부를 것이다.
a와 b를 포함한 사이의 모든 숫자의 범위를 [a,b]로 표기한다. a와 b를 포함하지 않는 경우 (a,b)로 표기한다. 위 두 가지를 포함하여 [a,b)로 a는 포함하고 b는 포함하지 않는 경우를 표기할 수 있다.
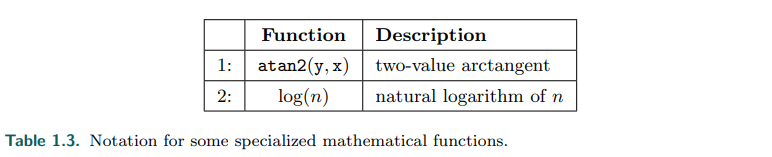
C-math의 atan2(y,x) 함수는 책에서 자주 사용된다. 이 함수는 수학적인 함수 arctan(x)의 확장이다. 두 함수의 차이점은 다음과 같다.

atan2함수에는 여분의 인수가 더 추가된 식이다. 흔히 arctan를 arctan(y/x)의 용도로 사용하는데, x = 0이게 되면 0으로 나누는 결과가 발생한다. atan2(y,x)의 추가된 인수가 이를 피할 수 있게 해준다.
여기서 log(n) 표기의 밑은 10이 아니라 항상 자연 로그(e)를 의미한다.
3차원 컴퓨터그래픽스에서 좌표계는 오른손 좌표계를 사용한다. 벡터 3요소의 색상은 요소의 크기가 [0,1]인 (red, green, blue)으로 표현한다.
1.2.2 기하학적 정의
기본적인 렌더링의 기본요소(drawing primitives라고도 함)에서는 거의 대부분의 모든 그래픽 하드웨어에서 점, 선, 삼각형이 사용된다.
이 책에서, 기하학적인 요소들을 model 또는 object로 말 할 것이다. scene은 모든 것을 구성하는 model들의 모임을 말한다. 이것도 렌더링 환경에 포함된다. scene은 material 묘사, lighting, viewing에 대한 자세한 정보들을 포함한다.
차나 건물 도로와 같은 objects를 예로 들어보자. 실제로, object는 항상 렌더링의 기본요소들로 구성되진 않을 수도 있다. object가 Bezier curves or surfaces(베지에 곡선이나 표면) 또는 subdivision surfaces(세분면) 같은 높은 수준의 기하학적인 결과물일 수도 있다. 또한, objects는 다른 objects로 구성될 수도 있다. 가령 네 개의 문 object, 네 개의 휠 object 등을 가진 차 object와 같이 말이다.
1.2.3 Shading (음영)
이 책에서 앞으로 볼 컴퓨터 그래픽에서 사용하는 단어는 "shading", "shader"에서 파생되었고, 두 개의 구분되지만 연관된 개념인 computer-generated visual appearance(컴퓨터로 제작된 시각적 외형, "shading model", "shading equation", "toon shading" 등)이나 programmable component of rendering system(프로그램할 수 있는 렌더링 시스템의 요소, "vertex shader", "shading language" 등)를 참조하는데 사용되는 단어이다. 이 두 경우로 단어가 쓰일 때, 문맥에서 의도한 것을 명확히 알아야한다..
추가 서적 및 자료
참조할 수 있는 가장 중요한 자료는 이 책의 사이트 realtimerendering.com이다. 링크에는 최신정보와 각 장에 대한 것들이 포함되어있다. real-time rendering의 분야는 실시간으로 변화하고 있다. 책에서는 기본적인 개념과 유행에 뒤떨어지지 않는 기술들에 초점을 맞추려 하였다. 웹사이트에서 오늘날 SW 개발자와 관련있는 정보를 줄 기회를 제공하고, 충분히 계속해서 업데이트할 수 있다.
'개발 · 컴퓨터공학' 카테고리의 다른 글
| UNIX system call - create (0) | 2021.09.16 |
|---|---|
| UNIX - File permissions 파일 권한 (0) | 2021.09.15 |
| UNIX system call - open (0) | 2021.09.14 |
| UNIX의 파일체계 (0) | 2021.09.13 |
| 네트워크 프로그래밍 - TCP 소켓 프로그래밍의 시작 (0) | 2021.09.12 |


