Hash가 사용되는 곳
export default class ClothSelfCollision extends Collision {
...
solve(dt: number) {
...
for (let id0 = 0; id0 < this.numParticles; id0++) {
if (this.invMass[id0] == 0.0) continue;
const adjacentParticles = this.hash.getAdjacentParticles(id0);collision solve에서 인접 particle을 구하는 과정 뿐 아니라
export class ClothPhysicsObject extends PhysicsObject {
...
preIntegration(dt: number) {
this.hash.create(this.positions);
this.hash.queryAll(this.positions, ((1 / 60) * 0.2 * this.thickness) / dt);
}cloth physics object class 안에서 preIntegration을 할 때도 hash기법이 사용된다
알고리즘은 안한지 정말 오래되서 hash의 개념을 까먹었지만 다시 보자
/**
* Hash table for self collisions of the Cloth object
*
* https://github.com/matthias-research/pages/blob/master/tenMinutePhysics/11-hashing.pdf
* https://www.carmencincotti.com
*/
export class Hash {
...carmen씨가 Hash class를 개발할 때 주로 matthias muller씨의 이론을 참고하였다
matthias muller씨는 물리 시뮬레이션 분야의 거장이기 때문에 참고해보도록 하자
Hashing

n개의 particle. 여기서는 point라고 하자
목표는 point \(p_i\)들에 대해서 거리 \(d\) 안에 있는 인접 particle \(p_j\) 들을 찾는 것이다
만약 \(d=2r\)로 거리가 지름보다 작은 걸 찾으면 overlap되는 것들에 대한 조건이 된다
이런 조건은 보통 유체, 모래, 눈 시뮬레이션 등에서 사용된다
naive solution

naive하게는 이렇게 pseudo code로 표현할 수 있다
naive 하다는 것은 연산량이 많다는 것. 복잡도는 \(O(n^2)\)에 달한다
얼마나 연산이 많냐면, 100,000 즉 십만개의 point는 10,000,000,000. 100억 번 연산한다..
일반적으로 1억당 1초니까 한 번 시뮬레이션 처리를 하는데 100초씩 걸린다는 이야기이다.. ㄷㄷ
차라리 \(O(n)\)이나 \(O(n\,log\;n)\)이라면 괜찮다
Grid Hashing 방법
point들을 계산하기에 위의 naive 방법은 너무 연산량이 많으니 새로운 방법이 고안되었다
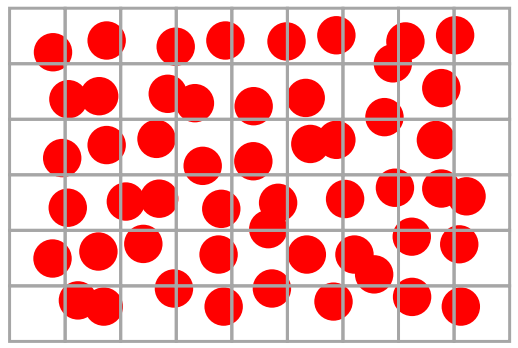
바로 grid cell에 particle 들을 저장해놓고 hashing을 이용해서 연산하는 방법이다
과정을 알아보자
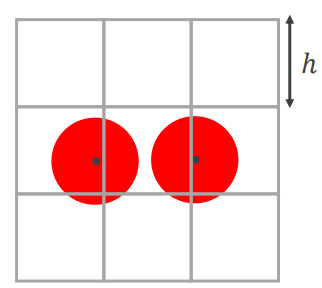
먼저 particle의 중심이 위치한 곳을 position으로 저장할 것이다
한 grid의 길이는 h인데, 여기서 \(h=2r\)로 정하면 particle을 포함하는 cell 즉 칸들을 확인해야한다
Grid 저장하기

$$x_i = Math.floor(p_x / spacing)$$
$$y_i = Math.floor(p_y / spacing)$$
우선 grid안에서 paritcle의 위치 좌표 \(x_i \; y_i\)에 대해서 정의한다. position값에서 spacing 한 칸의 길이를 나누어서 x,y좌표 인덱스를 정의한 것이다.
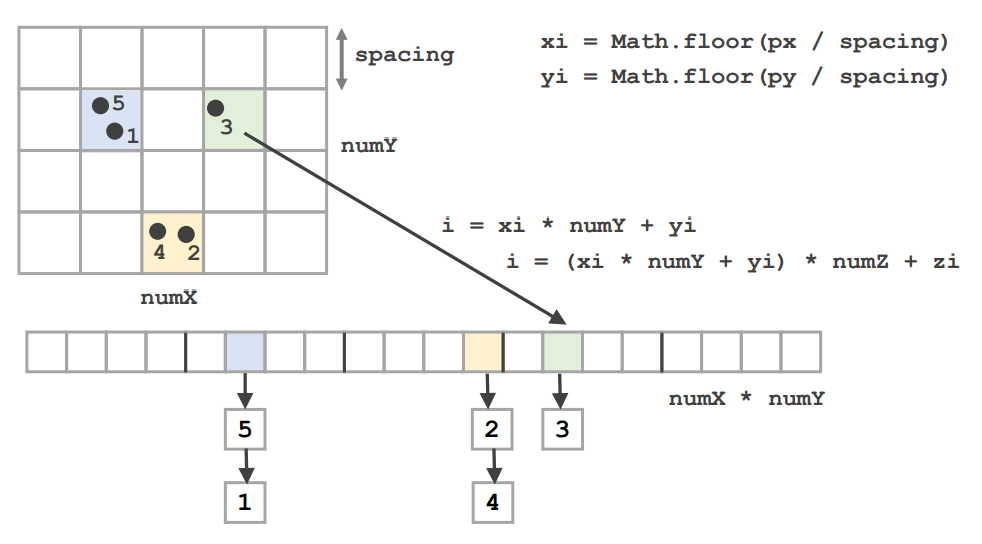
그러고 나면 정의한 x좌표 y좌표를 가지고 새로운 index \(i\)를 만든다
이 새로운 index \(i\)는 particle들을 저장하는 \( numX \cdot numY \) array에서 index \(i\)번째에 저장하게 된다
2차원 grid에서는 다음 수식으로 i를 결정한다
$$ i = x_i \cdot numY + y_i $$
예를들어 그림에서 초록칸에 있는 3번 particle을 예시로 들어보자
세로가 4칸이므로 \(numY=4\)이고
3번 입자의 \(x_i\)는 왼쪽에서 4번째 칸이므로 3이다
\(y_i\)는 위에서 2번째 칸이므로 1이다
즉 식에 대입하면 \(3 \cdot 4 + 1 = 13\)이라서
13번째 인덱스에 3번 particle이 들어간다
참고로, 3차원 grid의 경우 다음 수식을 이용한다
$$ i = (x_i \cdot numY + y_i) \cdot numZ + z_i $$
Grid 밀도 표현하기
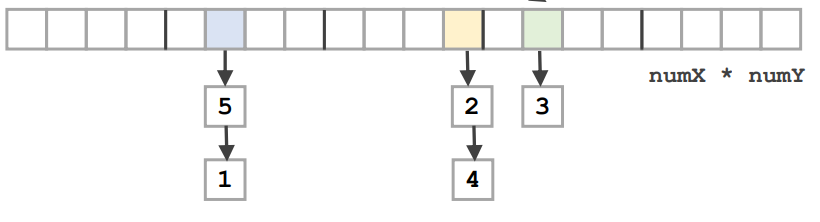
위에서 이러한 형태의 array에 particle을 저장하고 나면
다음 단계에서는 단계별로 증가하는 밀도 수치를 적는다
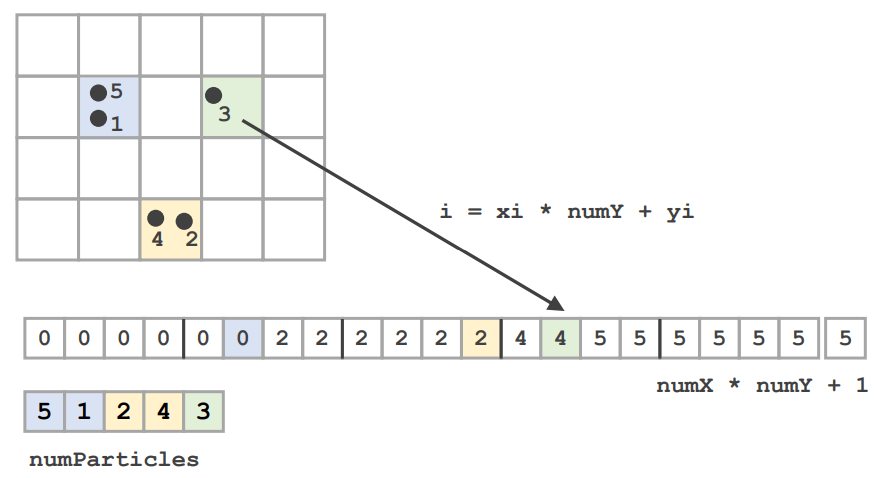
이게 무슨 말인지 모르겠어서 생각을 좀 해봤는데,
단순하게는 (0,0)부터 한 칸 한 칸 씩 이동하면서 쌓인 총 particle의 개수를 세는 일이다
특이하게도 마지막 인덱스를 하나 추가한다
이 총 개수는 어디에 필요하냐
아직은 모르겠다
범위가 특정되지 않은 Grid의 경우
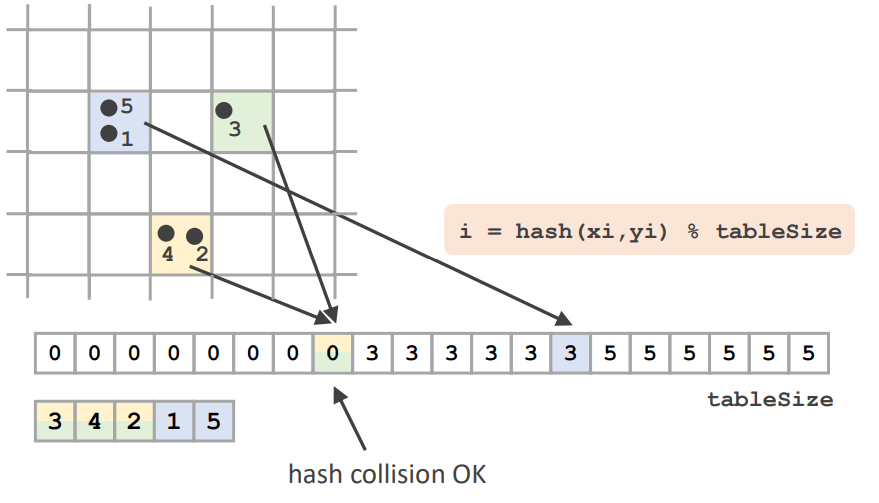
딱 떨어져서 경계가 없는 무한히 넓은 Grid 안에서
특정 table만을 정해서 그 안의 particle들을 배열에 넣을 때 위 그림처럼 hashing을 사용하면
다른 cell의 particle들이 같은 array index에 들어가버리는 hash collision이 발생한다
일단 두 cell의 array index가 같아지는 경위가 어떻게 되냐
이번에 array index \(i\)를 구하는 방법으로 hash 함수를 사용하고,
그 값을 tableSize(array length)로 나누어 index를 구한다
hashing 기법을 이용한다면 충돌은 피하기 어려운 단점이다
hashing 함수
hashCoords(xi, yi, zi) {
var h = (xi * 92837111) ^ (yi * 689287499) ^ (zi * 283923481);
return Math.abs(h) % this.numCells;
}hash 함수를 보자
일단 3차원 기준으로 만들어진 hash 함수인데 각 좌표 인덱스에는 랜덤한 큰 소수를 곱한다
각 좌표 인덱스에 곱했으면 이것들을 XOR 비트 연산자로 합한다 (hashing 기법의 일환이니 여기서 이유를 찾지 않는다)
그리고 array size로 나눈것 처럼 hash 함수 안에서도 numCells 변수로 모듈러 연산을 한다
hash 함수의 특징 중 table size 즉 numCells를 크게하면 충돌나는 경우가 현저히 줄고, 적은 테스트로도 빠른 연산을 할 수 있다
hash 자료 구조 만들기

hash 함수로 만들어지는 자료 구조를 보자
table을 array로 하여 particle 개수를 표현한 count와 그 누적인 partial sums
fill in을 보면 어떤 순서로 담고 있는건지 헷갈린다
일단 partial sums를 가지고 시작한다
partial sums에서 particle이 들어가있는 index의 count 값을 하나씩 줄이고
줄인 count 값을 numParticles의 index로 지정해서 particle 번호를 넣는다
이게 무슨 말이냐..
예시를 들면 이렇다
1번 particle을 어디에 넣을지는 partial sums에서 1번 particle이 위치한 index 5(파란색 칸)의 count수가 정한다
count를 하나 줄여서 1이 되므로 numParticles 배열에서 index 1에 해당하는 칸에 1번 particle을 넣는다
2번 particle도 마찬가지. index 11(노란색)의 count를 줄여서 3이므로, numParticles 배열의 index 3에 넣는다
같은 방식으로 쭉 진행한다
이렇게 복잡한 과정으로 얻은 numParticles는 어디에 쓰이는 걸까..
마무리
다음 포스팅에서는 직접 Hash.ts 스크립트를 보면서 어떻게 cloth simulation에서 hash 함수를 사용하였는지 코드로 확인해보자


