Super Bible에서 사용하는 sb6라이브러리에는 vmath라는 컴포넌트가 있는데, 이를 이용해서 벡터와 행렬을 다루는 데 사용할 수 있다. 행렬과 벡터 연산을 직접 하지 않아도 해당 컴포넌트를 이용하면 수월히 진행할 수 있지만, 개념은 아는 것이 좋을 것이다.
typedef Tvec3<float> vec3;
typedef Tvec4<float> vec4;vmath namespace에는 벡터와 위와 같은 형태로 정의되어 있고, 다음과 같이 선언할 수 있다.
vmath::vec3 vVector;
/// or
using namespace vmath;
vec3 vVector;
constructor와 copy operator는 다음과 같다.
vec3 vmath::vVertex1(0.0f, 0.0f, 1.0f);
vec4 vmath::vVertex2 = vec4(1.0f, 0.0f, 1.0f, 1.0f);
vec4 vmath::vVertex3(vVertex1, 1.0f);
vec3 vmath::vVerts[] = { vmath::vec3(-0.5f, 0.0f, 0.0f),
vmath::vec3(0.5f, 0.0f, 0.0f),
vmath::vec3(0.0f, 0.5f, 0.0f) } ;위와 같은 방법으로 삼각형을 이루는 3요소 vertex array를 선언할 수 있다.
많은 경우, geometry vertex위치를 설정하는데 3요소 vertex로 충분하고, surface normal vector의 경우도 3요소 vecter면 충분하지만 행렬에서는 네 번째 요소인 w가 필요하여 4 x 4로 변환할 필요가 있다.
Common Vector Operators
기본적인 연산은 다음과 같다.
vmath::vec3 a(1.0f, 2.0f, 3.0f);
vmath::vec3 b(4.0f, 5.0f, 6.0f);
vmath::vec3 c;
c = a + b;
c = a - b;
c += b;
c = -c;Dot Product
Dot Product(내적)는 사이각에 대한 코사인에 두 벡터 길이를 곱하여 scalar값을 리턴한다. 만약 두 벡터 사이의 실제 각을 구하기 위해서는 arc-cosine을 사용한다.
dot product는 lighting에서 많이 사용되는데, diffuse lighting에서 surface normal 벡터와 light source 뱡향 벡터에 대해 사용된다.

벡터를 이용한 내적 연산은 다음과 같다.
V1 × V2 = V1.x × V2.x + V1.y × V2.y + V1.z × V2.z
vmath::vec3 a(...);
vmath::vec3 b(...);
float c = a.dot(b);
float d = dot(a, b);내적을 위한 함수는 vmath에서 dot라는 함수를 이용할 수 있다.
float angle(const vmath::vec3& u, const vmath::vec3& v);vmath의 angle 함수는 두 벡터 사이의 각을 라디안으로 변환하는 함수이다.
Cross Product
cross product(외적)는 두 벡터의 수직인 다른 벡터를 구한다.
V1 × V2 = ||V1|| ||V2|| sin(θ)n
위 식에서 n은 v1 v2에 모두 수직인 단위벡터이고, 결과를 정규화하면 두 벡터로 이루어지는 평면에 수직인 벡터를 얻는다.

외적 연산은 위와 같이 진행하고,

그림으로 보면 이렇다.
vmath 라이브러리에는 다음과 같은 외적 함수를 제공한다.
vec3 a(...);
vec3 b(...);
vec3 c = a.cross(b);
vec3 d = cross(a, b);이 경우 a, b의 순서에 따라 결과는 달라진다.
외적은 삼각형의 surface normal을 찾는 것에서 부터 변환 행렬 생성까지 다양하게 사용된다.
Length of a Vector

template <typename T, int len>
static inline T length(const vecN<T,len>& v) { ... }벡터의 길이를 구하는 vmath 함수이다.
Reflection and Refraction
reflection과 refraction은 그래픽스에서 자주 사용하는 연산이다.
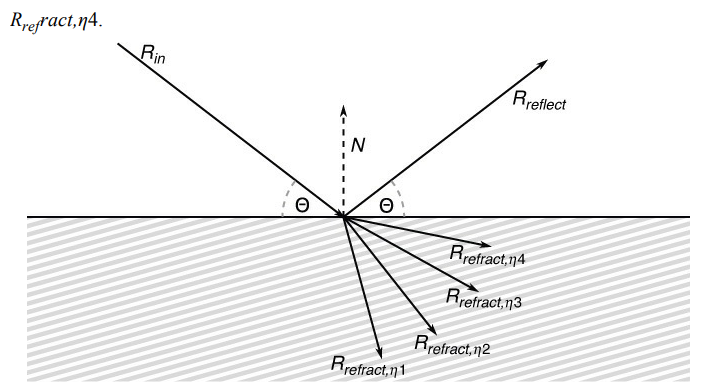

reflection를 계산하는 식은 위와 같고,

refraction을 계산하는 식은 위와 같다.
위 두 연산에 있어서 R과 N은 모두 정규화된 단위 길이 벡터이어야한다.
Matrices
행렬에 대한 개념은 자세히 다루지 않고 vmath의 함수만 보겠다.
vmath::mat2 m1;
vmath::mat3 m2;
vmath::mat4 m3;각각 2x2, 3x3, 4x4의 행렬이 선언되어있다.
Matrix Construction and Operators
GLfloat matrix[16]; // Nice OpenGL-friendly matrix
GLfloat matrix[4][4]; // Not as convenient for OpenGL programmers행렬 생성자에 있어. 위 두 방식 모두 사용할 수 있다.
Understanding Transformations
3D그래픽스는 2D데이터로 projection한 데이터를 화면에 표시하는 것이다. OpenGL에서는 projection도 여러 변환 기법 중 하나이다.
Coordinate Spaces in OpenGL
3D 그래픽스에서 사용되는 일반적인 좌표 공간은 다음과 같은 것들이 있다.
Model space
로컬 원점에 상대적인 위치, 때로는 Object space라고도 한다.
World space
global 원점에 상대적인 위치.
Lighting 계산이나 Physics 계산이 일어나는 공간이다.
View space
viewer에 상대적인 위치, camera space 또는 eye space라고도 한다.


위 그림으로 설명할 수 있다. 왼쪽 그림은 viewer가 움직였을 때 view space이고, 오른쪽은 view space가 사용되는 엔진에서의 가상의 고정 좌표계이다.
OpenGL에서는 cartesian 좌표계를 사용하여 변환이 없는 경우 view space와 동일하다.
Clip space
projection 후 비선형 homogeneous coordinate에서 버텍스들의 위치. 즉 clipping을 수행하는 공간이다.
vertex shader가 gl_Position에 쓸 때를 clip space에 있다고 하고, clip space를 떠날 때 w요소로 vertex가 나누어져 normalized device 좌표로 가게된다.
Normalized device coordinate space
clip space 좌표를 w요소로 나눈 vertex 좌표.
window space
window의 원점에 상대적인 픽셀 상의 vertex 위치.
Coordinate Transformations

그림에서와 같이 오브젝트를 움직이고, 회전하고, 스케일을 변경하는 등 여러가지 변환이 있을 수 있다.
이러한 변환은 행렬로 표현할 수 있고, vertex 좌표에 곱하여 변환 후 위치를 계산할 수 있다.
The Identity Matrix
첫 번째로 단위 행렬이 있다.

단위 행렬은 위 그림과 같이 대각선만 1이고, 나머지는 0인 행렬이다.
위 행렬을 곱하여도 행렬은 변하지 않는다.
// Using a raw array:
GLfloat m1[] = { 1.0f, 0.0f, 0.0f, 0.0f, // X Column
0.0f, 1.0f, 0.0f, 0.0f, // Y Column
0.0f, 0.0f, 1.0f, 0.0f, // Z Column
0.0f, 0.0f, 0.0f, 1.0f }; // W Column
// Or using the vmath::mat4 constructor:
vmath::mat4 m2{ vmath::vec4(1.0f, 0.0f, 0.0f, 0.0f), // X Column
vmath::vec4(0.0f, 1.0f, 0.0f, 0.0f), // Y Column
vmath::vec4(0.0f, 0.0f, 1.0f, 0.0f), // Z Column
vmath::vec4(0.0f, 0.0f, 0.0f, 1.0f) }; // W Column위와 같이 생성할 수도 있겠지만, vmath 라이브러리에도 위 행렬을 생성하는 함수들이 있다.
vmath::mat2 m2 = vmath::mat2::identity();
vmath::mat3 m3 = vmath::mat3::identity();
vmath::mat4 m4 = vmath::mat4::identity();vertex shader에서 pass-through shader로 사용하는 경우 이러한 단위 행렬을 사용한다.
The Translation Matrix

하나 이상의 축의 방향으로 이동시키는 이동 행렬이다.

위와 같은 공식을 따르며 t는 각 축의 이동을 나타낸다.

위 구조를 보면 homogeneous 좌표를 사용하는 이유를 알 수 있다. w가 1.0인 vector v에 이동 행렬을 곱한 결과이다.
t가 v의 요소에 더해져서 이동을 수행한다. 만약 v 벡터의 w가 1.0이 아니라면 t가 해당 값으로 scale되어 결과에 영향을 준다. 때문에 위치 벡터는 일반적으로 w요소가 1.0이다.
방향벡터의 경우 w요소가 없거나 0으로 저장한다.
template <typename T>
static inline Tmat4<T> translate(T x, T y, T z) { ... }
template <typename T>
static inline Tmat4<T> translate(const vecN<T,3>& v) { ... }OpenGL에서는 위 함수를 통해 vec3 혹은 각각의 요소를 인자로 이동 행렬을 수행할 수 있다.
The Rotation Matrix
임이의 벡터에 대해 회전시킬 때 rotation matrix가 필요하다.

x축에 따른 회전은 위 행렬을 사용한다. 세타는 각도이다.

마찬가지로 각각 y, z축에 대한 회전에 필요한 행렬이다.

세 축에 대한 행렬을 한 번에 곱하면 위와 같은 단일 행렬-벡터 곱 연산으로 할 수 있다.
R함수 안의 기호는 각도, s는 sin, c는 cos이다.
template <typename T>
static inline Tmat4<T> rotate(T angle_x, T angle_y, T_angle_z);이렇게 vmath가 쉽게 도와준다.
template <typename T>
static inline Tmat4<T> rotate(T angle, T x, T y, T z);
template <typename T>
static inline Tmat4<T> rotate(T angle, const vecN<T,3>& axis);위 함수는 축을 기준으로 회전하는 것이다.
vmath::mat4 rotation_matrix = vmath::rotate(45.0, 1.0, 1.0, 1.0);위 예시는 vertex (1,1,1)로 지정한 축 주위로 45도 회전하는 행렬을 생성한다.

이렇게 말이다. 함수의 내부적으로는 degree를 radian으로 변경해서 처리된다.
Euler Angles
Euler Angles은 공간상 회전을 나타내는 세 각도의 집합이다. 각 축 별로 얼마나 회전을 하였는지 행렬이 담고 있다고 생각하면 된다.
gimbal lock을 아는가 특정 축에 대해 회전시키다가 다른 축과 겹친 이후로 두 축이 정렬되어 같이 움직이는 현상이다.
그래서 x, y, z에 대해서 회전을 누적하는 오일러 방식보다도 각-축 방식이나 Quaternion으로 표현하고 필요한 경우에 행렬로 변환한다.
The Scaling Matrix
standard transformation 행렬이다.

위와 같은 형태로 scaling 행렬이 이루어져있고, s는 scale값을 나타낸다.
template <typename T>
static inline Tmat4<T> scale(T x, T y, T z) { ... }
template <typename T>
static inline Tmat4<T> scale(const Tvec3<T>& v) { ... }
template <typename T>
static inline Tmat4<T> scale(T x) { ... }vmath에서는 위와 같은 방식으로 표현된다. x, y, z 축의 scale 값을 넘기거나, vec3를 인자로 사용하거나, 인자 하나를 세 축에 대해서 모두 적용시킨다.
Concatenating Transformations
행렬의 연속적인 곱은 연속적인 변환이다.
vmath::mat4 translation_matrix = vmath::translate(4.0f, 10.0f, -20.0f);
vmath::mat4 rotation_matrix = vmath::rotate(45.0f,
vmath::vec3(0.0f, 1.0f,
0.0f));
vmath::vec4 input_vertex = vmath::vec4(...);
vmath::vec4 transformed_vertex = translation_matrix *
rotation_matrix *
input_vertex;
vmath나 OpenGL코드를 작성할 때, 벡터를 행렬에 곱하고 변환 행렬들을 역순으로 확인한다.
위 코드의 경우 먼저 y축에 대해 45도 rotate하고, x축에 대해 4만큼, y축에 대해 10만큼 z축에 대해 -20만큼 translate한다. 회전 다음에 이동한다. 즉 코드의 역순이 동작 순서이다.
vmath::mat4 translation_matrix = vmath::translate(4.0f, 10.0f, -20.0f);
vmath::mat4 rotation_matrix = vmath::rotate(45.0f,
vmath::vec3(0.0f, 1.0f,
0.0f));
vmath::mat4 composite_matrix = translation_matrix * rotation_matrix;
vmath::vec4 input_vertex = vmath::vec4(...);
vmath::vec4 transformed_vertex = composite_matrix *
input_vertex;두 과정을 composite_matrix로 합성하여 위 코드처럼 할 수 있다.
Quaternions
quaternion은 4차원 quantity의 개념이다.

실수부 하나와 허수부 3개로 이루어져 있다. i, j, k가 허수부이다.


위와 같은 복소수의 허수부같은 특징이있다.

두 쿼터니언의 곱은 위와 같이 구하고, 이는 교환법칙이 성립하지 않는다.

위처럼 한 개의 실수부 r과 세 개의 허수부 v 벡터로 표현하기도 한다.
연속적인 회전도 쿼터니언의 여러 곱으로 수행할 수 있는데, 쿼터니언으로 인한 연산의 경우 짐벌락이 발생하지 않는다.
vmath의 quaternion클래스로 이용할 수 있다.
The Model–View Transform
모델 변환은 객체를 월드 공간으로이동시킨다. 모델 공간의 vertex 위치에 모델 변환을 곱한 결과는 월드 공간상의 위치이기 때문에, 모델-월드 변환이라고도 한다.
뷰 변환은 관측점 위치와 방향을 잡을 수 있다. 이는 장면에 카메라를 위치시키는 일과 유사하다. 작업하는 결과물들이 뷰에서 확인할 수 있어야 하므로 뷰 변환이 다른 변환보다 먼저가 되어야한다. 좌표계를 월드 공간에서 뷰 공간으로 이동시키는 변환을 월드-뷰 변환이라고 한다.
위 두 변환 행렬을 곱하여 합성한 것이 모델-뷰 행렬이다. 두 변환을 각각 하는 것보다 효율적이고, 뷰어로부터 얼마나 떨어져있는가에 따라서 객체의 vertex를 계산하는 정밀도가 가까울 경우 높게, 멀리있는 경우 낮게 부여될 수 있다.
The Lookat Matrix
카메라가 향하려는 지점과 방향이 있을 때 해당 방향으로 올바르게 바라보게 하고 카메라의 초점(중심)을 이동하도록 하는 변환이다. lookat matrix를 사용한다.
두 위치 좌표의 뺄셈으로 해당 위치로 이동하는 벡터를 만들어 정규화하면, 카메라가 바라보아야 할 전방벡터를 구할 수 있다.
전방 벡터와 좌표계에서 위를 향하는 벡터를 이용해서 외적을 부하면 카메라의 옆 방향 벡터를 구할 수 있다.
카메라 옆 방향 벡터와 전방 벡터를 이용해서 카메라의 시점에서 위를 향하는 벡터를 구할 수 있다.
구한 세 좌표로 뷰 좌표계를 구성한다.



위 식들은 위 문단에서 언급한 과정을 수식으로 나타낸 것이다. e는 카메라위치, p는 대상의 위치, f가 전방벡터, u가 월드 좌표계의 위 벡터, s가 옆 벡터, u'이 카메라의 위 벡터이다.


객체의 행렬 R에서
가장 오른쪽 행에 이동값 e를 음수로 넣으면 lookat 행렬 T를 만들 수 있다.
template <typename T>
static inline Tmat4<T> lookat(const vecN<T,3>& eye,
const vecN<T,3>& center,
const vecN<T,3>& up) { ... }vmath 라이브러리로는 위와 같은 함수를 사용하여 행렬을 구한다.
Projection Transformations
프로젝션 변환은 모델-뷰 변환 후 vertex에 적용되는 변환이다. 뷰 볼륨을 정의하고 클리핑 평면을 정의하는데, 클리핑 평면은 OpenGL이 geometry가 보이나 판단하기 위한 3D 공간에서의 평면 공식이다. 이해가 잘 안되는데, 간단히 말해 뷰와 모델링이 끝난 작업이 화면상의 최종 이미지로 투영되는 것을 결정한다. orthographic과 perspective가 있다.
정사영(orthographic)은 평행하게 투영하여 거리와는 상관없이 2차원 이미지로 렌더링된다.
원근 투영(perspective)은 원근감을 느낄 수 있는 투영방법이다. 원근감을 느끼기 위해 객체에 특별한 처리 없이도 모델-뷰 변환 후 원근 투영 행렬을 적용하면 가능하다.

Perspective Matrices
뷰 공간안에 있는 vertex를 projection 행렬을 통해 투영한다. 원근 행렬로는 frustum maxtrix하고 각뿔을 자른 모양인 절두체(frustum)를 사용한다.

원근 행렬은 위와 같은 형태를 지니는데, 아직은 잘 모르겠다.
static inline mat4 frustum(float left,
float right,
float bottom,
float top,
float n,
float f) { ... }vmath에는 frustum함수가 있다. 각 인자들을 통해 frustum의 형태를 결정하는데 n은 near, f는 far로 근거리 평면, 원거리평면에 대한 값이다.
static inline mat4 perspective(float fovy /* in degrees */,
float aspect,
float n,
float f) { ... }vmath perspective함수로는 대칭적인 frustum만 만들 수 있다.
Orthographic Matrices
정사영이 필요하다면 정사영 행렬을 찾자.

위와 같은 형태이고,
static inline mat4 ortho(float left,
float right,
float bottom,
float top,
float near,
float far) { ... }vmath의 함수는 ortho로 행렬을 구할 수 있다.




